Fermat’s Last Theorem extends to negative Integers

I bumped into Fermat’s Last Theorem the other day, probably the most famous margin note in history:

a^n+b^n=c^n

Where a, b, c and n are all positive integers. The equation has no solutions for n>2.

But the theorem always constrains a, b and c to be positive. Why?

Here’s what I found plugging in -a and -b scenarios into the formula.

First, if n is even, (-a)^n=a^n so this returns us to the positive Integer version of Fermat’s Last Theorem.

Conversely, if n is odd and we have both -a and -b, then:

(-a)^{n_{odd}}+(-b)^{n_{odd}}=-(a^{n_{odd}}+b^{n_{odd}})

This is just the negative version of Fermat’s Last Theorem, so it follows again there’s no solution for n>2.

Next, I discovered an infinite number of solutions for the equation to any odd power. If we set b=-a, this leads to:

a^{n_{odd}}+(-a)^{n_{odd}}=a^{n_{odd}}-a^{n_{odd}}=0^{n_{odd}}

Let’s just declare that solution “trivial” and move on. So the final leftover scenario is this:

a^{n_{odd}}+(-b)^{n_{odd}}=c^{n_{odd}}

Which can be rearranged to this:

a^{n_{odd}}=b^{n_{odd}}+c^{n_{odd}}

And this, of course, is just another rewrite of Fermat’s Last Theorem.

So throwing away the trivial case that b=-a with n_{odd} it quickly becomes clear that the theorem is true for all negative numbers with n>2. Which still makes me wonder why the theorem is always stated “for positive a, b and c“?

PS. When I was initially googling to find other work on this question nothing relevant popped up (leaving me to figure out how negative numbers work in the theorem myself). However, I found other interesting proofs. Here’s a  simple proof extending Fermat’s Last Theorem to all positive rationals a and b:

Write Fermat’s Last Theorem with rationals:

(\frac{a}{x})^n+(\frac{b}{y})^n=(\frac{c}{z})^n

Multiply through by xyz which recovers the original Fermat’s Last Theorem:

(ayz)^n+(bxz)^n=(cxy)^n

My reasoning for negative Integers applies equally well to the negative Rationals.

So, throwing out trivial solutions, Fermat’s Last Theorem is true for all Integers and Rationals, not just the positive ones.

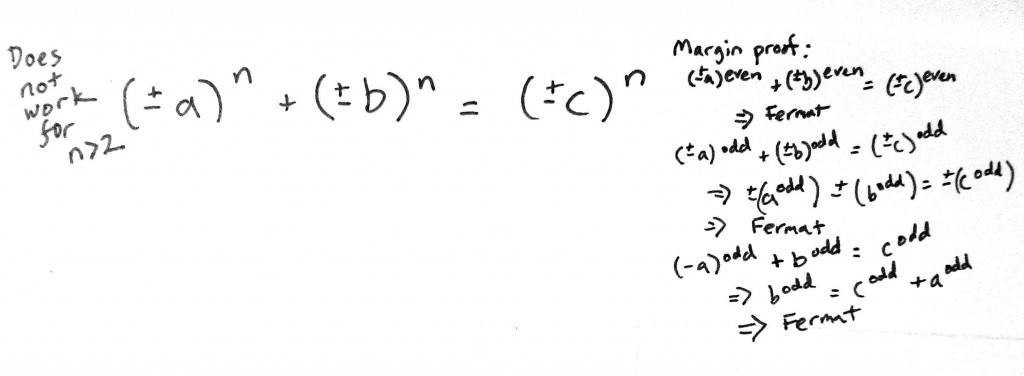
fermat_with_neg_numbers

4 Comments

  1. Dear author, there is a small flaw in the post. Please note that FERMAT’S LAST THEOREM is true for all integers, except for 0, as using 0 might allow us to break his theorem. Regards, VARSHA SURESH

  3. Dear author, i have a proof for this theorem, which i suppose to be true. Is there anyway through which i can share my proof with you? Please do let me know. Thank you.

Leave a Reply

Your email address will not be published. Required fields are marked *